
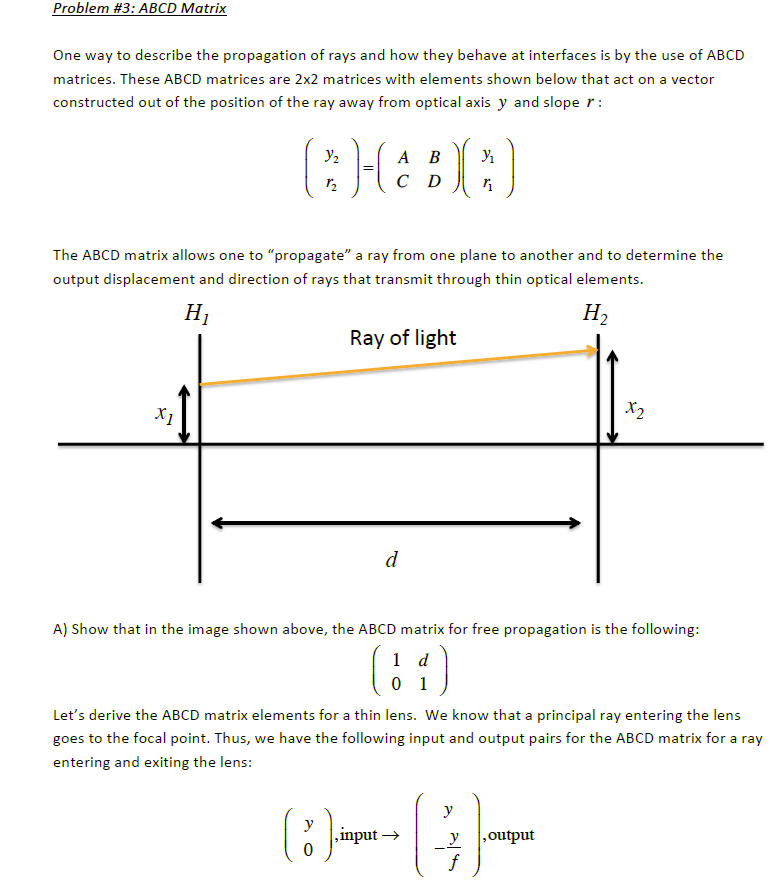
What is particularly noteworthy about the angle of the ray after the transformation?Īnd the answering of these questions should show you how the transfer matrix encodes the lens's collimating behavior for all points on the focal plane. case, Moshinsky and Quesne have shown a decomposition of a symplectic ABCD-matrix with a singular B, as a cascade of two matrices that do not have such a.So your task is to work out what the transfer matrix in (1) does to this state, i.e. Before we begin, I believe your transfer matrix should be: In fact, you compute the image given the object position by using the unique, fixed transfer matrix characterizing an optical element. matrices pertinent to periodic optical systems, where the equi-diagonalization is achieved by a similarity transformation using. So it doesn't depend at all on where the object and image are. The ray transfer matrix (also known as the ABCD matrix) is used in geometrical optics for ray-tracing analysis. An alternative tool in the frequency domain is the transfer function, which defines how a circuit network can act like an amplifier or filter. So why would you consider using ABCD parameters The answer is simple ABCD matrices can be cascaded to provide the performance of two cascaded networks, S. As such, it is meant to work for all cases, at least approximately, over a range of inputs. S-parameter measurements are commonly used to characterize high-speed and high-frequency circuits in the frequency domain. so that the total voltage and current at port i can be expressed as follows: Vi V+ i +V i Z oi ai +bi C 2a Ii I+ i I i 1 Z oi aibi C 2b and, from (1. In ABCD matrix analysis (also known as Ray transfer matrix analysis) a 2-by-2 matrix associated with an optical element is used to describe the element's effect on a light ray. There is not uniqueness of the solution for the matrix inversion. The third line represents an unbalanced system where N i > N e. It is found that the M 2 factor increases linearly with the on axis phase shift.A transfer matrix is a representation of a homogeneous linear function that approximates a behavior. A 2049 ABCD matrices as similarity transformations of Wigner matrices and periodic systems in optics S. The matrix inversion has to be done with the pseudo-inverse operator ( +). In addition, it is demonstrated that the emerging beam from the Kerr lens is no longer Gaussian since its propagation factor M 2 is larger than unity. V n-is the amplitude of the voltage wave reflected from port n.
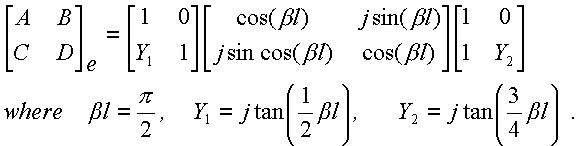
The expression of the focal length associated with the Kerr lens that we have obtained is in a good agreement with the expression of the focal length determined on the basis of a Zernike decomposition. THE SCATTERING MATRIX V n + is the amplitude of the voltage wave incident on port n. There is another set of network parameters particularly suited. The latter has been numerically determined from a numerical diffraction analysis, and we have empirically found that the right focal length is obtained by multiplying, by a factor equal to 3, the focal length given by the usual parabolic approximation. S parameters are useful for describing interactions of voltage and current waves with a network.

The Kerr focal length deduced from the ABCD formalism is found to not correctly provide the focal plane position. other known analyzing techniques like SWOC, Competitive Profile Matrix (CPM) analysis, EFE & IFE Matrices, BCG analysing frameworks, Porters Five Forces Model, and PESTLE Analysis. The usual parabolic approximation used for modelling the focusing properties of a Kerr lens induced by a Gaussian laser beam, through optical Kerr effect, consists to roughly approximate a Gaussian profile by a parabola.


 0 kommentar(er)
0 kommentar(er)
